Comparing Floating Point Numbers, 2012 Edition

This post is a more carefully thought out and peer reviewed version of a floating-point comparison article I wrote many years ago. This one gives solid advice and some surprising observations about the tricky subject of comparing floating-point numbers. A compilable source file with license is available.

We’ve finally reached the point in this series that I’ve been waiting for. In this post I am going to share the most crucial piece of floating-point math knowledge that I have. Here it is:

[Floating-point] math is hard.

You just won’t believe how vastly, hugely, mind-bogglingly hard it is. I mean, you may think it’s difficult to calculate when trains from Chicago and Los Angeles will collide, but that’s just peanuts to floating-point math.

Seriously. Each time I think that I’ve wrapped my head around the subtleties and implications of floating-point math I find that I’m wrong and that there is some extra confounding factor that I had failed to consider. So, the lesson to remember is that floating-point math is always more complex than you think it is. Keep that in mind through the rest of the post where we talk about the promised topic of comparing floats, and understand that this post gives some suggestions on techniques, but no silver bullets.

Previously on this channel…

This is the fifth chapter in a long series. The first couple in the series are particularly important for understanding this point. A (mostly) complete list of the other posts includes:

• 1: Tricks With the Floating-Point Format – an overview of the float format
• 2: Stupid Float Tricks – incrementing the integer representation
• 3: Don’t Store That in a Float – a cautionary tale about time
• 3b: They sure look equal… – ranting about Visual Studio’s float failings
• 4: Comparing Floating Point Numbers, 2012 Edition (return *this;)
• 5: Float Precision–From Zero to 100+ Digits – non-obvious answers to how many digits of precision a float has
• 6: C++ 11 std::async for Fast Float Format Finding – running tests on all floats in just a few minutes
• 7: Intermediate Floating-Point Precision – the surprising complexities of how expressions can be evaluated
• 8: Floating-point complexities – some favorite quirks of floating-point math
• 9: Exceptional Floating Point – using floating point exceptions for fun and profit
• 10: That’s Not Normal–the Performance of Odd Floats – the performance implications of infinities, NaNs, and denormals
• 11: Doubles are not floats, so don’t compare them – a common type of float comparison mistake
• 12: Float Precision Revisited: Nine Digit Float Portability – moving floats between gcc and VC++ through text
• 13: Floating-Point Determinism – what does it take to get bit-identical results
• 14: There are Only Four Billion Floats–So Test Them All! – exhaustive testing to avoid embarrassing mistakes
• 15: Please Calculate This Circle’s Circumference – the intersection of C++, const, and floats
• 16: Intel Underestimates Error Bounds by 1.3 quintillion – the headline is not an exaggeration, but it’s not as bad as it sounds

Comparing for equality

Floating point math is not exact. Simple values like 0.1 cannot be precisely represented using binary floating point numbers, and the limited precision of floating point numbers means that slight changes in the order of operations or the precision of intermediates can change the result. That means that comparing two floats to see if they are equal is usually not what you want. GCC even has a (well intentioned but misguided) warning for this: “warning: comparing floating point with == or != is unsafe”.

Here’s one example of the inexactness that can creep in:

float f = 0.1f;
float sum;
sum = 0;

for (int i = 0; i < 10; ++i)
    sum += f;
float product = f * 10;
printf("sum = %1.15f, mul = %1.15f, mul2 = %1.15f\n",
        sum, product, f * 10);

This code tries to calculate ‘one’ in three different ways: repeated adding, and two slight variants of multiplication. Naturally we get three different results, and only one of them is 1.0:

sum=1.000000119209290, mul=1.000000000000000, mul2=1.000000014901161

Disclaimer: the results you get will depend on your compiler, your CPU, and your compiler settings, which actually helps make the point.

So what happened, and which one is correct?

What do you mean ‘correct’?

Before we can continue I need to make clear the difference between 0.1, float(0.1), and double(0.1). In C/C++ the numbers 0.1 and double(0.1) are the same thing, but when I say “0.1” in text I mean the exact base-10 number, whereas float(0.1) and double(0.1) are rounded versions of 0.1. And, to be clear, float(0.1) and double(0.1) don’t have the same value, because float(0.1) has fewer binary digits, and therefore has more error. Here are the exact values for 0.1, float(0.1), and double(0.1):

Number	Value
0.1	0.1 (of course)
float(.1)	0.100000001490116119384765625
double(.1)	0.10000000000000000555111512312578270211815834045 41015625

With that settled, let’s look at the results of the code above:

1. sum = 1.000000119209290: this calculation starts with a rounded value and then adds it ten times with potential rounding at each add, so there is lots of room for error to creep in. The final result is not 1.0, and it is not 10 * float(0.1). However it is the next representable float above 1.0, so it is very close.
2. mul = 1.000000000000000: this calculation starts with a rounded value and then multiplies by ten, so there are fewer opportunities for error to creep in. It turns out that the conversion from 0.1 to float(0.1) rounds up, but the multiplication by ten happens to, in this case, round down, and sometimes two rounds make a right. So we get the right answer for the wrong reasons. Or maybe it’s the wrong answer, since it isn’t actually ten times float(0.1) !
3. mul2 = 1.000000014901161: this calculation starts with a rounded value and then does a double-precision multiply by ten, thus avoiding any subsequent rounding error. So we get a different right answer – the exact value of 10 * float(0.1) (which can be stored in a double but not in a float).

So, answer one is incorrect, but it’s only one float away. Answer two is correct (but inexact), whereas answer three is completely correct (but appears wrong).

Now what?

Now we have a couple of different answers (I’m going to ignore the double precision answer), so what do we do? What if we are looking for results that are equal to one, but we also want to count any that are plausibly equal to one – results that are “close enough”.

Epsilon comparisons

If comparing floats for equality is a bad idea then how about checking whether their difference is within some error bounds or epsilon value, like this:

bool isEqual = fabs(f1 – f2) <= epsilon;

With this calculation we can express the concept of two floats being close enough that we want to consider them to be equal. But what value should we use for epsilon?

Given our experimentation above we might be tempted to use the error in our sum, which was about 1.19e-7f. In fact, there’s even a define in float.h with that exact value, and it’s called FLT_EPSILON.

Clearly that’s it. The header file gods have spoken and FLT_EPSILON is the one true epsilon!

Except that that is rubbish. For numbers between 1.0 and 2.0 FLT_EPSILON represents the difference between adjacent floats. For numbers smaller than 1.0 an epsilon of FLT_EPSILON quickly becomes too large, and with small enough numbers FLT_EPSILON may be bigger than the numbers you are comparing (a variant of this led to a flaky Chromium test)!

For numbers larger than 2.0 the gap between floats grows larger and if you compare floats using FLT_EPSILON then you are just doing a more-expensive and less-obvious equality check. That is, if two floats greater than 2.0 are not the same then their difference is guaranteed to be greater than FLT_EPSILON. For numbers above 16777216 the appropriate epsilon to use for floats is actually greater than one, and a comparison using FLT_EPSILON just makes you look foolish. We don’t want that.

Relative epsilon comparisons

The idea of a relative epsilon comparison is to find the difference between the two numbers, and see how big it is compared  to their magnitudes. In order to get consistent results you should always compare the difference to the larger of the two numbers. In English:

To compare f1 and f2 calculate diff = fabs(f1-f2). If diff is smaller than n% of max(abs(f1),abs(f2)) then f1 and f2 can be considered equal.

In code:

bool AlmostEqualRelative(float A, float B,
                         float maxRelDiff = FLT_EPSILON)
{
    // Calculate the difference.
    float diff = fabs(A - B);
    A = fabs(A);
    B = fabs(B);
    // Find the largest
    float largest = (B > A) ? B : A;

    if (diff <= largest * maxRelDiff)
        return true;
    return false;
}

This function is not bad. It works. Mostly. I’ll talk about the limitations later, but first I want to get to the point of this article – the technique that I first suggested many years ago.

When doing a relative comparison of floats it works pretty well to set maxRelDiff to FLT_EPSILON, or some small multiple of FLT_EPSILON. Anything smaller than that and it risks being equivalent to no epsilon. You can certainly make it larger, if greater error is expected, but don’t go crazy. However selecting the correct value for maxRelativeError is a bit tweaky and non-obvious and the lack of a direct relationship to the floating point format being used makes me sad.

ULP, he said nervously

We already know that adjacent floats have integer representations that are adjacent. This means that if we subtract the integer representations of two numbers then the difference tells us how far apart the numbers are in float space. That brings us to:

Dawson’s obvious-in-hindsight theorem:

If the integer representations of two same-sign floats are subtracted then the absolute value of the result is equal to one plus the number of representable floats between them.

In other words, if you subtract the integer representations and get one, then the two floats are as close as they can be without being equal. If you get two then they are still really close, with just one float between them. The difference between the integer representations tells us how many Units in the Last Place the numbers differ by. This is usually shortened to ULP, as in “these two floats differ by two ULPs.”

So let’s try that concept:

/* See
https://randomascii.wordpress.com/2012/01/11/tricks-with-the-floating-point-format/
for the potential portability problems with the union and bit-fields below.
*/

#include <stdint.h> // For int32_t, etc.

union Float_t
{
    Float_t(float num = 0.0f) : f(num) {}
    // Portable extraction of components.
    bool Negative() const { return i < 0; }
    int32_t RawMantissa() const { return i & ((1 << 23) - 1); }
    int32_t RawExponent() const { return (i >> 23) & 0xFF; }

    int32_t i;
    float f;
#ifdef _DEBUG
    struct
    {   // Bitfields for exploration. Do not use in production code.
        uint32_t mantissa : 23;
        uint32_t exponent : 8;
        uint32_t sign : 1;
    } parts;
#endif
};

bool AlmostEqualUlps(float A, float B, int maxUlpsDiff)
{
    Float_t uA(A);
    Float_t uB(B);

    // Different signs means they do not match.
    if (uA.Negative() != uB.Negative())
    {
        // Check for equality to make sure +0==-0
        if (A == B)
            return true;
        return false;
    }

    // Find the difference in ULPs.
    int ulpsDiff = abs(uA.i - uB.i);
    if (ulpsDiff <= maxUlpsDiff)
        return true;
    return false;
}

This is tricky and perhaps profound.

The check for different signs is necessary for several reasons. Subtracting the signed-magnitude representation of floats using twos-complement math isn’t particularly meaningful, and the subtraction would produce a 33-bit result and overflow. Even if we deal with these technical issues it turns out that an ULPs based comparison of floats with different signs doesn’t even make sense.

Even a ridiculously small number, like 1e-30 has an ‘large’ integer representation of 228,737,632. So, while 1e-30 is ‘close’ to zero and ‘close’ to negative 1e-30 it is a gargantuan distance from those numbers in ULPs.

After the special cases are dealt with we simply subtract the integer representations, get the absolute value, and now we know how different the numbers are. The ‘ulpsDiff’ value gives us the number of floats between the two numbers (plus one) which is a wonderfully intuitive way of dealing with floating-point error.

One ULPs difference good (adjacent floats).

One million ULPs difference bad (kinda different).

Comparing numbers with ULPs is really just a way of doing relative comparisons. It has different characteristics at the extremes, but in the range of normal numbers it is quite well behaved. The concept is sufficiently ‘normal’ that boost has a function for calculating the difference in ULPs between two numbers.

A one ULP difference is the smallest possible difference between two numbers. One ULP between two floats is far larger than one ULP between two doubles, but the nomenclature remains terse and convenient. I like it.

ULP versus FLT_EPSILON

It turns out checking for adjacent floats using the ULPs based comparison is quite similar to using AlmostEqualRelative with epsilon set to FLT_EPSILON. For numbers that are slightly above a power of two the results are generally the same. For numbers that are slightly below a power of two the FLT_EPSILON technique is twice as lenient. In other words, if we compare 4.0 to 4.0 plus two ULPs then a one ULPs comparison and a FLT_EPSILON relative comparison will both say they are not equal. However if you compare 4.0 to 4.0 minus two ULPs then a one ULPs comparison will say they are not equal (of course) but a FLT_EPSILON relative comparison will say that they are equal.

This makes sense. Adding two ULPs to 4.0 changes its magnitude twice as much as subtracting two ULPs, because of the exponent change. Neither technique is better or worse because of this, but they are different.

If my explanation doesn’t make sense then perhaps my programmer art will:

ULP based comparisons also have different performance characteristics. ULP based comparisons are more likely to be efficient on architectures such as SSE which encourage the reinterpreting of floats as integers. However ULPs based comparisons can cause horrible stalls on other architectures, due to the cost of moving float values to integer registers. These stalls generally happen when doing float calculations and then immediately doing ULP based comparisons on the results, so keep that in mind when benchmarking.

Normally a difference of one ULP means that the two numbers being compared have similar magnitudes – the larger one is usually no larger than 1.000000119 times larger than the smaller. But not always. Some notable exceptions are:

• FLT_MAX to infinity – one ULP, infinite ratio
• zero to the smallest denormal – one ULP, infinite ratio
• smallest denormal to the next smallest denormal – one ULP, two-to-one ratio
• NaNs – two NaNs could have very similar or even identical representations, but they are not supposed to compare as equal
• Positive and negative zero – two billion ULPs difference, but they should compare as equal
• As discussed above, one ULP above a power of two is twice as big a delta as one ULP below that same power of two

That’s a lot of notable exceptions. For many purposes you can ignore NaNs (you should be enabling illegal operation exceptions so that you find out when you generate them) and infinities (ditto for overflow exceptions) so that leaves denormals and zeros as the biggest possible problems. In other words, numbers at or near zero.

Infernal zero

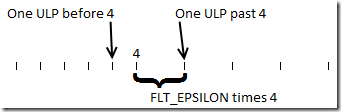
It turns out that the entire idea of relative epsilons breaks down near zero. The reason is fairly straightforward. If you are expecting a result of zero then you are probably getting it by subtracting two numbers. In order to hit exactly zero the numbers you are subtracting need to be identical. If the numbers differ by one ULP then you will get an answer that is small compared to the numbers you are subtracting, but enormous compared to zero.

Consider the sample code at the very beginning. If we add float(0.1) ten times then we get a number that is obviously close to 1.0, and either of our relative comparisons will tell us that. However if we subtract 1.0 from the result then we get an answer of FLT_EPSILON, where we were hoping for zero. If we do a relative comparison between zero and FLT_EPSILON, or pretty much any number really, then the comparison will fail. In fact, FLT_EPSILON is 872,415,232 ULPs away from zero, despite being a number that most people would consider to be pretty small.

For another example, consider this calculation:

float someFloat = 67329.234; // arbitrarily chosen
float nextFloat = 67329.242; // exactly one ULP away from ‘someFloat’
bool equal = AlmostEqualUlps( someFloat, nextFloat, 1); // returns true, numbers 1 ULP apart

Our test shows that someFloat and nextFloat are very close – they are neighbors. All is good. But consider what happens if we subtract them:

float diff = (nextFloat – someFloat); // .0078125000
bool equal = AlmostEqualUlps( diff, 0.0f, 1 ); // returns false, diff is 1,006,632,960 ULPs away from zero

While someFloat and nextFloat are very close, and their difference is small by many standards, ‘diff’ is a vast distance away from zero, and will dramatically and emphatically fail any ULPs or relative based test that compares it to zero.

There is no easy answer to this problem. If you think you have found an easy and generic answer to this problem then you should re-read the material above.

The most generic answer to this quandary is to use a mixture of absolute and relative epsilons. If the two numbers being compared are extremely close – whatever that means – then treat them as equal, regardless of their relative values. This technique is necessary any time you are expecting an answer of zero due to subtraction. The value of the absolute epsilon should be based on the magnitude of the numbers being subtracted – it should be something like maxInput * FLT_EPSILON. Unfortunately this means that it is dependent on the algorithm and the inputs. Charming.

The ULPs based technique also breaks down near zero for the technical reasons discussed just below the definition of AlmostEqualUlps.

Doing a floating-point absolute epsilon check first, and then treating all other different-signed numbers as being non-equal is the simpler and safer thing to do. Here is some possible code for doing this, both for relative epsilon and for ULPs based comparison, with an absolute epsilon ‘safety net’ to handle the near-zero case:

bool AlmostEqualUlpsAndAbs(float A, float B,
            float maxDiff, int maxUlpsDiff)
{
    // Check if the numbers are really close -- needed
    // when comparing numbers near zero.
    float absDiff = fabs(A - B);
    if (absDiff <= maxDiff)
        return true;

    Float_t uA(A);
    Float_t uB(B);

    // Different signs means they do not match.
    if (uA.Negative() != uB.Negative())
        return false;

    // Find the difference in ULPs.
    int ulpsDiff = abs(uA.i - uB.i);
    if (ulpsDiff <= maxUlpsDiff)
        return true;
    return false;
}

bool AlmostEqualRelativeAndAbs(float A, float B,
            float maxDiff, float maxRelDiff = FLT_EPSILON)
{
    // Check if the numbers are really close -- needed
    // when comparing numbers near zero.
    float diff = fabs(A - B);
    if (diff <= maxDiff)
        return true;

    A = fabs(A);
    B = fabs(B);
    float largest = (B > A) ? B : A;

    if (diff <= largest * maxRelDiff)
        return true;
    return false;
}

Catastrophic cancellation, hiding in plain sight

If we calculate f1 – f2 and then compare the result to zero then we know that we are dealing with catastrophic cancellation, and that we will only get zero if f1 and f2 are equal. However, sometimes the subtraction is not so obvious.

Consider this code:

sin(pi);

It’s straightforward enough. Trigonometry teaches us that the result should be zero. But that is not the answer you will get. For double-precision and float-precision values of pi the answers I get are:

sin(double(pi)) = +0.00000000000000012246467991473532
sin(float(pi))     = -0.000000087422776

If you do an ULPs or relative epsilon comparison to the ‘correct’ value of zero then this looks pretty bad. It’s a long way from zero. So what’s going on? Is the calculation of sin() really that inaccurate?

Nope. The calculation of sin() is pretty close to perfect – in recent glibc versions it is perfect. Even Intel’s fsin instruction, which gives an answer with just a few bits of precision in this case, still gets the correct order of magnitude. The problem is not with sin()/fsin – the problem lies elsewhere. But to understand what’s going on we have to invoke… calculus!

For a deeper analysis of Intel’s fsin instruction see Intel Underestimates Error Bounds by 1.3 quintillion

But first we have to acknowledge that we aren’t asking the sin function to calculate sin(pi). Instead we are asking it to calculate sin(double(pi)) or sin(float(pi)). Since pi is transcendental and irrational it should be no surprise that pi cannot be exactly represented in a float, or even in a double.

Therefore, what we are really calculating is sin(pi-theta), where theta is a small number representing the difference between ‘pi’ and float(pi) or double(pi).

Calculus teaches us (since the derivative of sin(pi) is negative one) that, for sufficiently small values of theta, sin(pi-theta) == theta. Therefore, if our sin function is sufficiently accurate we would expect sin(double(pi)) to be roughly equal to pi-double(pi). In other words, sin(double(pi)) actually calculates the error in double(pi)! This is best shown for sin(float(pi)) because then we can easily add float(pi) to sin(float(pi)) using double precision:

float(pi)	+3.1415927410125732
sin(float(pi))	-0.0000000874227800
float(pi) + sin(float(pi))	+3.1415926535897966

If you haven’t memorized pi to 15+ digits then this may be lost on you, but the salient point is that float(pi) + sin(float(pi)) is a more accurate value of pi than float(pi). Or, alternately, sin(float(pi)) tells you nothing more than the error in float(pi).

Woah. Dude.

Again: sin(float(pi)) equals the error in float(pi).

I’m such a geek that I think that is the coolest thing I’ve discovered in quite a while.

Think about this. Because this is profound. Here are the results of comparing sin(‘pi’) to the error in the value of ‘pi’ passed in:

sin(double(pi)) = +0.0000000000000001224646799147353207
pi-double(pi)   = +0.0000000000000001224646799147353177
sin(float(pi))  = -0.000000087422776
pi-float(pi)    = -0.000000087422780

Wow. Our predictions were correct. sin(double(pi)) is accurate to sixteen to seventeen significant figures as a measure of the error in double(pi), and sin(float(pi)) is accurate to six to seven significant figures. The main reason the sin(float(pi)) results are less accurate is because operator overloading translates this to (float)sin(float(pi)) which rounds the result to float precision.

I think it is perversely wonderful that we can use double-precision math to precisely measure the error in a double precision constant. Visual C++ 2015 can print the value of double(pi) to arbitrarily many digits, and glibc now calculates pi() accurately, so we can use this code and some hand adding to calculate pi to over 30 digits of accuracy!

double pi = 3.14159265358979323846;
printf(“%.35f\n%.35f\n”,pi,sin(pi));

3.14159265358979311599796346854418516
0.00000000000000012246467991473532072

You can also see this trick in action with a calculator. Just put it in radians mode, try these calculations, and note how the input plus the result add up to pi. Nerdiest bar trick ever:

pi =3.1415926535…

sin(3.14)
=0.001592652
sin(3.1415)
=0.000092654
sin(3.141502050)
=0.000090603

The point is, that sin(float(pi)) is actually calculating pi-float(pi), which means that it is classic catastrophic cancellation. We should expect an absolute error (from zero) of up to about 3.14*FLT_EPSILON/2, and in fact we get a bit less than that.

Know what you’re doing

There is no silver bullet. You have to choose wisely.

• If you are comparing against zero, then relative epsilons and ULPs based comparisons are usually meaningless. You’ll need to use an absolute epsilon, whose value might be some small multiple of FLT_EPSILON and the inputs to your calculation. Maybe.
• If you are comparing against a non-zero number then relative epsilons or ULPs based comparisons are probably what you want. You’ll probably want some small multiple of FLT_EPSILON for your relative epsilon, or some small number of ULPs. An absolute epsilon could be used if you knew exactly what number you were comparing against.
• If you are comparing two arbitrary numbers that could be zero or non-zero then you need the kitchen sink. Good luck and God speed.

Above all you need to understand what you are calculating, how stable the algorithms are, and what you should do if the error is larger than expected. Floating-point math can be stunningly accurate but you also need to understand what it is that you are actually calculating. If you want to learn more about algorithm stability you should read up on condition numbers and consider getting Michael L Overton’s excellent book Numerical Computing with IEEE Floating Point Arithmetic. If your code is giving large errors then, rather than increasing your epsilon values, you should try restructuring your code to make it more stable – this can sometimes give stunning results.

The true value of a float

In order to get the results shown above I used the same infinite precision math library I created for Fractal eXtreme to check all the math and to print numbers to high precision. I also wrote some simple code to print the true values of floats and doubles. Next time I’ll share the techniques and code used for this extended precision printing – unlocking one more piece of the floating-point puzzle, and explaining why, depending on how you define it, floats have a decimal precision of anywhere from one to over a hundred digits.

Now that VC++ 2015 can print the exact value of floats and doubles it is trivial for Windows developers to print the exact value represented by a float or double. Being able to see the exact value of numbers such as double(0.1) can help make sense of some tricky floating-point math problems.

Credits

Thanks to Florian Wobbe for his excellent error finding and many insights into this topic.

Other references:

• Josh Haberman’s floating-point summary, part 1
• Floating-point converter tool
• The original floating-point-comparison article, with all of its flaws