That’s Not Normal–the Performance of Odd Floats

Denormals, NaNs, and infinities round out the set of standard floating-point values, and these important values can sometimes cause performance problems. The good news is, it’s getting better, and there are diagnostics you can use to watch for problems.

In this post I briefly explain what these special numbers are, why they exist, and what to watch out for.

This article is the last of my series on floating-point. The complete list of articles in the series is:

• 1: Tricks With the Floating-Point Format – an overview of the float format
• 2: Stupid Float Tricks – incrementing the integer representation of floats
• 3: Don’t Store That in a Float – a cautionary tale about time
• 3b: They sure look equal… – special bonus post (not on altdevblogaday)
• 4: Comparing Floating Point Numbers, 2012 Edition – tricky but important
• 5: Float Precision—From Zero to 100+ Digits – what does precision mean, really?
• 5b: C++ 11 std::async for Fast Float Format Finding – special bonus post (not on altdevblogaday) on fast scanning of all floats
• 6: Intermediate Precision – their effect on performance and results
• 7.0000001: Floating-Point Complexities – a lightning tour of all that is weird about floating point
• 8: Exceptional Floating point – using floating-point exceptions to find bugs
• 9: That’s Not Normal–the Performance of Odd Floats

The special float values include:

Infinities

Positive and negative infinity round out the number line and are used to represent overflow and divide-by-zero. There are two of them.

NaNs

NaN stands for Not a Number and these encodings have no numerical value. They can be used to represent uninitialized data, and they are produced by operations that have no meaningful result, like infinity minus infinity or sqrt(-1). There are about sixteen million of them, they can be signaling and quiet, but there is otherwise usually no meaningful distinction between them.

Denormals

Most IEEE floating-point numbers are normalized – they have an implied leading one at the beginning of the mantissa. However this doesn’t work for zero so the float format specifies that when the exponent field is all zeroes there is no implied leading one. This also allows for other non-normalized numbers, evenly spread out between the smallest normalized float (FLT_MIN) and zero. There are about sixteen million of them and they can be quite important.

If you start at 1.0 and walk through the floats towards zero then initially the gap between numbers will be 0.5^24, or about 5.96e-8. After stepping through about eight million floats the gap will halve – adjacent floats will be closer together. This cycle repeats about every eight million floats until you reach FLT_MIN. At this point what happens depends on whether denormal numbers are supported.

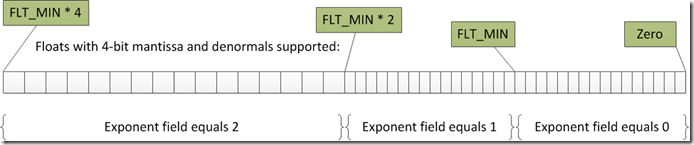
If denormal numbers are supported then the gap does not change. The next eight million numbers have the same gap as the previous eight million numbers, and then zero is reached. It looks something like the diagram below, which is simplified by assuming floats with a four-bit mantissa:

With denormals supported the gap doesn’t get any smaller when you go below FLT_MIN, but at least it doesn’t get larger.

If denormal numbers are not supported then the last gap is the distance from FLT_MIN to zero. That final gap is then about 8 million times larger than the previous gaps, and it defies the expectation of intervals getting smaller as numbers get smaller. In the not-to-scale diagram below you can see what this would look like for floats with a four-bit mantissa. In this case the final gap, between FLT_MIN and zero, is sixteen times larger than the previous gaps. With real floats the discrepancy is much larger:

If we have denormals then the gap is filled, and floats behave sensibly. If we don’t have denormals then the gap is empty and floats behave oddly near zero.

The need for denormals

One easy example of when denormals are useful is the code below. Without denormals it is possible for this code to trigger a divide-by-zero exception:

float GetInverseOfDiff(float a, float b) 
{ 
    if (a != b) 
        return 1.0f / (a - b); 
    return 0.0f; 
} 

This can happen because only with denormals are we guaranteed that subtracting two floats with different values will give a non-zero result.

To make the above example more concrete lets imagine that ‘a’ equals FLT_MIN * 1.125 and ‘b’ equals FLT_MIN. These numbers are both normalized floats, but their difference (.125 * FLT_MIN) is a denormal number. If denormals are supported then the result can be represented (exactly, as it turns out) but the result is a denormal that only has twenty-one bits of precision. The result has no implied leading one, and has two leading zeroes. So, even with denormals we are starting to run on reduced precision, which is not great. This is called gradual underflow.

Without denormals the situation is much worse and the result of the subtraction is zero. This can lead to unpredictable results, such as divide-by-zero or other bad results.

Even if denormals are supported it is best to avoid doing a lot of math at this range, because of reduced precision, but without denormals it can be catastrophic.

Performance implications on the x87 FPU

The performance of Intel’s x87 units on these NaNs and infinites is pretty bad. Doing floating-point math with the x87 FPU on NaNs or infinities numbers caused a 900 times slowdown on Pentium 4 processors. Yes, the same code would run 900 times slower if passed these special numbers. That’s impressive, and it makes many legitimate uses of NaNs and infinities problematic.

Even today, on a SandyBridge processor, the x87 FPU causes a slowdown of about 370 to one on NaNs and infinities. I’ve been told that this is because Intel really doesn’t care about x87 and would like you to not use it. I’m not sure if they realize that the Windows 32-bit ABI actually mandates use of the x87 FPU (for returning values from functions).

The x87 FPU also has some slowdowns related to denormals, typically when loading and storing them.

Historically AMD has handled these special numbers much faster on their x87 FPUs, often with no penalty. However I have not tested this recently.

Performance implications on SSE

Intel handles NaNs and infinities much better on their SSE FPUs than on their x87 FPUs. NaNs and infinities have long been handled at full speed on this floating-point unit. However denormals are still a problem.

On Core 2 processors the worst-case I have measured is a 175 times slowdown, on SSE addition and multiplication.

On SandyBridge Intel has fixed this for addition – I was unable to produce any slowdown on ‘addps’ instructions. However SSE multiplication (‘mulps’) on Sandybridge has about a 140 cycle penalty if one of the inputs or results is a denormal.

Denormal slowdown – is it a real problem?

For some workloads – especially those with poorly chosen ranges – the performance cost of denormals can be a huge problem. But how do you know? By temporarily turning off denormal support in the SSE and SSE2 FPUs with _controlfp_s:

#include <float.h> 
// Flush denormals to zero, both operands and results 
_controlfp_s( NULL, _DN_FLUSH, _MCW_DN ); 
… 
// Put denormal handling back to normal. 
_controlfp_s( NULL, _DN_SAVE, _MCW_DN );

This code does not affect the x87 FPU which has no flag for suppressing denormals. Note that 32-bit x86 code on Windows always uses the x87 FPU for some math, especially with VC++ 2010 and earlier. Therefore, running this test on a 64-bit process may provide more useful results.

If your performance increases noticeably when denormals are flushed to zero then you are inadvertently creating or consuming denormals to an unhealthy degree.

If you want to find out exactly where you are generating denormals you could try enabling the underflow exception, which triggers whenever one is produced. To do this in a useful way you would need to record a call stack and then continue the calculation, in order to gather statistics about where the majority of the denormals are produced. Alternately you could monitor the underflow bit to find out which functions set it. See Exceptional Floating Point for some thoughts on this, or read this paper.

Don’t disable denormals

Once you prove that denormals are a performance problem you might be tempted to leave denormals disabled – after all, it’s faster. But if it gives you a speedup means that you are using denormals a lot, which means that if you disable them you are going to change your results – your math is going to get a lot less accurate. So, while disabling denormals is tempting, you might want to consider investigating to find out why so many of your numbers are so close to zero. Even with denormals in play the accuracy near zero is poor, and you’d be better off staying farther away from zero. You should fix the root cause rather than just addressing the symptoms.